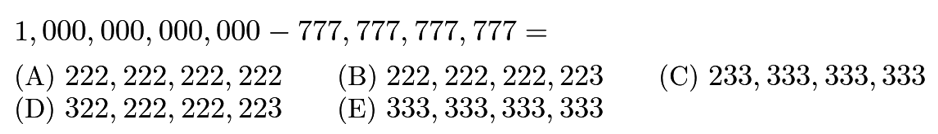
Answer: B
Solution:
=999,999,999,999-777,777,777,777+1=222,222,222,223.

Answer: C
Solution:
=24/2=12.

Answer: E
Solution:
200,000*200,000=40,000,000,000=40 billon.
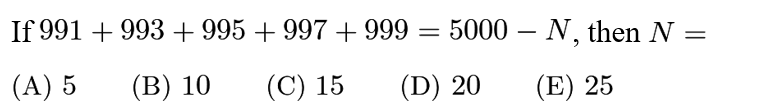
Answer: E
Solution:
991+993+995+997+999=995*5=4975=5000-25.
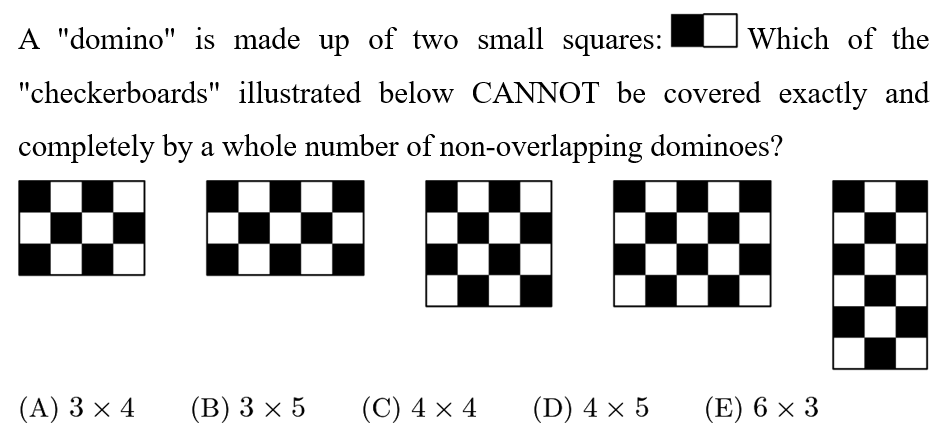
Answer: B
Solution:
For a bunch of dominoes to completely tile a board, the board must have an even number of squares. The 3*5 board clearly does not, so B cannot be tiled completely.

Answer: C
Solution:
The largest numbers in the first, second, third, fourth and fifth columns are 13,7,15,12,9, respectively. Of these, only 7 is the smallest in its row .

Answer: D
Solution:
=(500,000*12,000,000+9,000,000*500,000)/(20,000*0.05)
=(500,000*21,000,000)/1,000=(500,000*20,000,000)/1000=10,000,000,000

Answer: D
Solution:
Let the two chosen numbers be a and b, To maximize the quotient, we first have either a,b>0 or a,b<0, and from there we maximize |a| and minimize |b|.
For the case a,b<0, we have a=-24 and b=-2, which gives us (-24)/(-2)=12. For the case a,b>0, we have a=8 and b=1, which gives us 8/1=8. The answer is 12.

Answer: B
Solution:
There are 15 numbers divisible by 3; 9 numbers divisible by 5, so at first we have 15+9=24 numbers that are divisible by 3 or 5, except we counted the multiples of LCM(3,5)=15 twice, once for 3 and once for 5. There are 3 numbers divisible by 15, so there are 24-3=21 numbers divisible by 3 or 5.
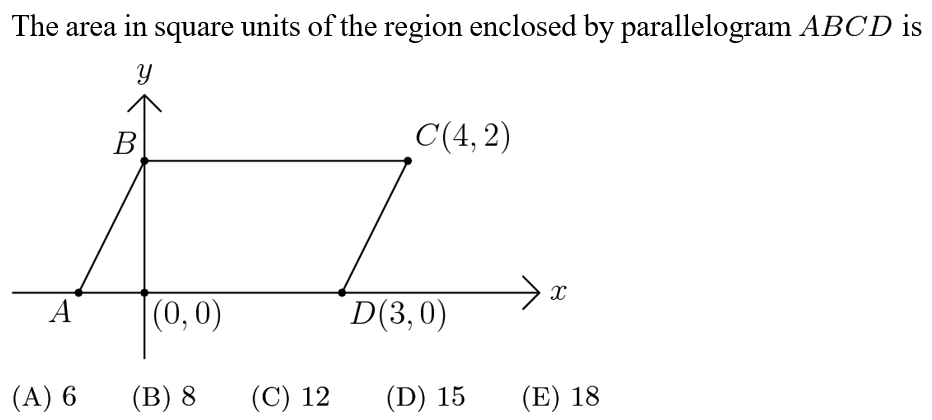
Answer: B
Solution:
The base is BC=4. The height has a length of the difference of the y-coordinates of A and B, which is 2. Therefore the area is 4*2=8.

Answer: B
Solution:
Let the three-element set be {a,b,c} and suppose that a=5. We need b+c=10 and b<>c. This gives us four solutions, so there are 4 sets with a 5 also with the desired properties.
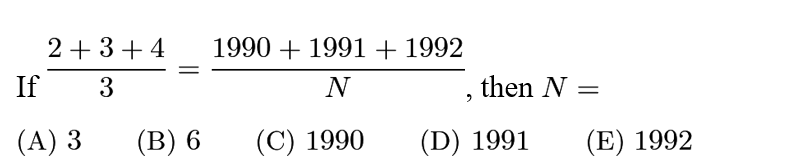
Answer: D
Solution:
Let the three-element set be {a,b,c} and suppose that a=5. We need b+c=10 and b<>c. This gives us four solutions, so there are 4 sets with a 5 also with the desired properties.
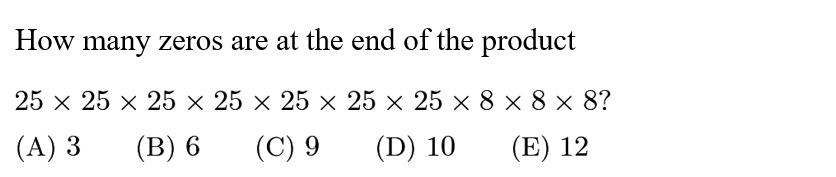
Answer: C
Solution:
=(5^2)^7 * (2^3)^3=5^14 * 2^9= 5^9 * 5^5 * 2^9= 5^9 * 2^9 * 5^5=(5*2)^9 * 5^5=10^9 * 5^5=25 * 10^9.

Answer: D
Solution:
There are two ways for a student to get 11: 5+5+1 and 5+3+3. Clearly if someone gets one of these combinations someone else could get the other, so we are not guaranteed the most points with 11.
There is only one way to get 13 points: 5+5+3. In this case, the largest score another person could get is 5+3+3, so having 13 points guarantees having more points than any other person .
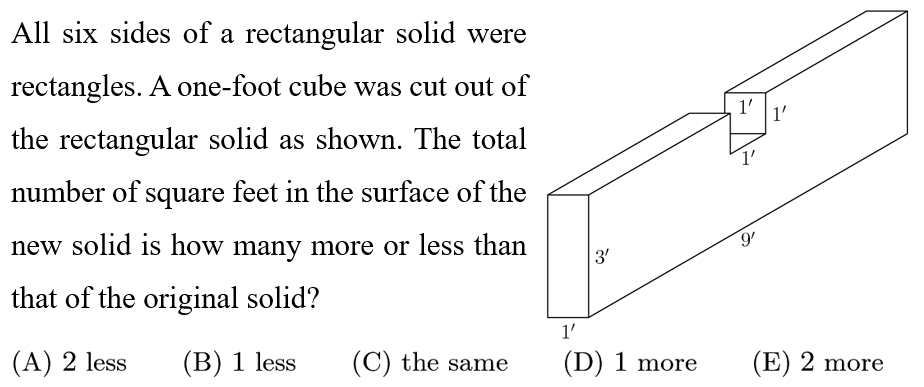
Answer: C
Solution:
Initially, that one-foot cube contributed 3 faces to the surface area of the whole solid. When it was removed, these 3 faces are removed, but there are 3 new faces where the cube was carved out, so the net change is 0.

Answer: B
Solution:
Suppose we undo each of the four folds, considering just the top square until we completely unfold the paper. x will be marked in the square if the face that shows after all the folds is face up, y if that face is facing down.

Answer: C
Solution:
If a row has 2k seats, clearly we can only fit k students in that row. If a row has 2k+1 seats, we can fit k+1 students by putting students at the ends and then alternating between skipping a seat and putting a student in.
For the 20 rows, there are corresponding 5, 6, 6, 7, 7, ……14,14, 15 seats in each row. The sum is 5+6+6+7+7+…+14+14+15=5+15+2*(6+7+…+14)=20+2*90=200.
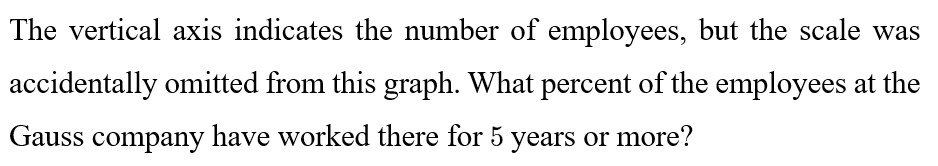
Answer: C
Solution:
Let x be the amount of people each x represents. The percent of people that worked for five or more years is then (2x+2x+2x+x+x+x)/(5x+5x+8x+3x+2x+2x+2x+x+x+x)=9x/30x=30%.

Answer: C
Solution:
If the average of the numbers is 10, then their sum is 10*10=100. To maximize the largest number of the ten, we minimize the other nine. Since they must be distinct, positive whole numbers, we let them be 1,2,3,4,5,6,7,8,9. Their sum is 45. The sum of nine of the numbers is 45, the sum of all ten is 100 so the last number must be 100-45=55.

Answer: A
Solution:
Using logic, a+b+c=10, and b+a+1(from the carry over)=10. So b+a=9 and a+1=3. Thus, a=2, and 11b+c=78, From here it becomes clear that b=7 and c=1.

Answer: A
Solution:
We know that T=20=32-3k =>k=4. V=24-4k=24-4*4=8.
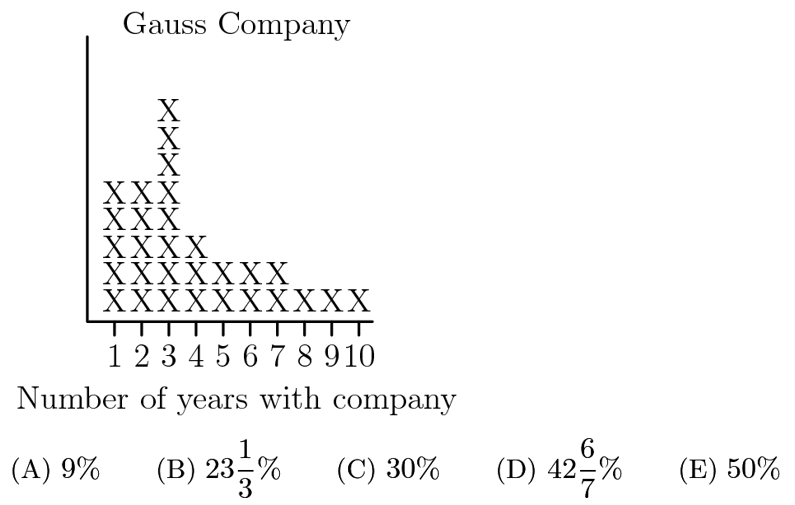
Answer: D
Solution:
Instead of computing this probability directly, we can find the probability that the product is odd, and subtract that from 1. The product of two integers is odd if and only if each of the two integers is odd. The probability the first spinner yields an odd number is 2/3 and the probability the second spinner yields an odd number is 1/3, so the probability both yield an odd number is 2/3 * 1/3=2/9. The desired probability is thus 1 – 2/9 =7/9.

Answer: A
Solution:
There are 100+80-60=120 females in either band or orchestra, so there are 230-120=110 males in either band or orchestra. Suppose x males are in both band and orchestra. 80+100-x=110 =>x=70. Thus, the number of males in band but not orchestra is 80-70=10.

Answer: E
Solution:
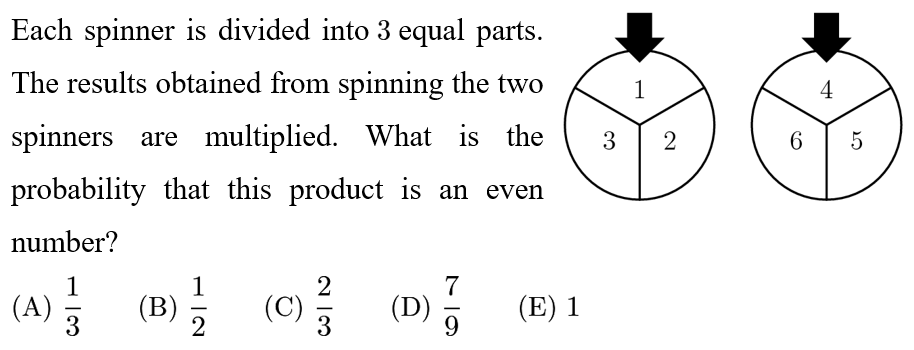
Answer: C
Solution:
With each change, 3/4 of the black space from the previous stage remains. Since there are 5 changes, the fractional part of the triangle that remains black is (3/4)^5=243/1024.
AMC培训、答疑,请联系微信 / 电话:136 1118 1627
艾蕾特教育 @Elite Edu, 在这里,